The Hyperbolic Geometry of Mental Space
20 March 2020
Created: 2020-03-20
Updated: 2020-11-07
Topics: Physics, Mathematics, Computer Science, Philosophy, Cognitive Science
Confidence: Highly Speculative
Status: Still in progress
TL;DR - Do you want to know how shadows, lettuce, brains, Escher, and Alice in Wonderland relate? I discuss the potential shape of one’s internal information, thoughts, values, rewards, and beliefs inside our Minds, and whether or not we can model these using Hyperbolic Geometry.

Recently I was experimenting with stereographic projection (a point-source of light rather than a parallel-source) of the hyperbolic sphere. Finding a stereographic projection is essentially equivalent to finding a mapping (aka a model) of the hyperbolic sphere to the Euclidean plane, allowing us to view what happens to the Schwarz triangle (2,3,7) tessellation or tiling pattern and how it warps. Notice that in our picture, although sizes and lengths are distorted, angles are the same.
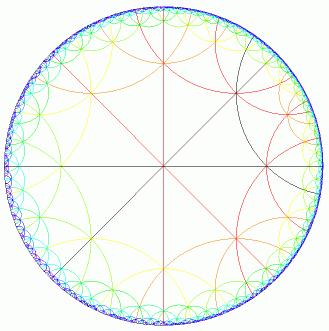
This occurs because the lines (called geodesics) that make up the sides of the triangle have to map from originally a circle that goes around a sphere (think similar to Earth’s equator) to either a single straight line or the many curved arcs radiating out from the edges of a upper half plane or flat surface.

Why study Hyperbolic geometry? Besides it being beautiful for beauty’s sake (indeed you can see this in Escher’s circle limit art due to collaboration with famous geometer Donald Coxeter), it is also a potential candidate for the underlying spatial geometry of our universe.
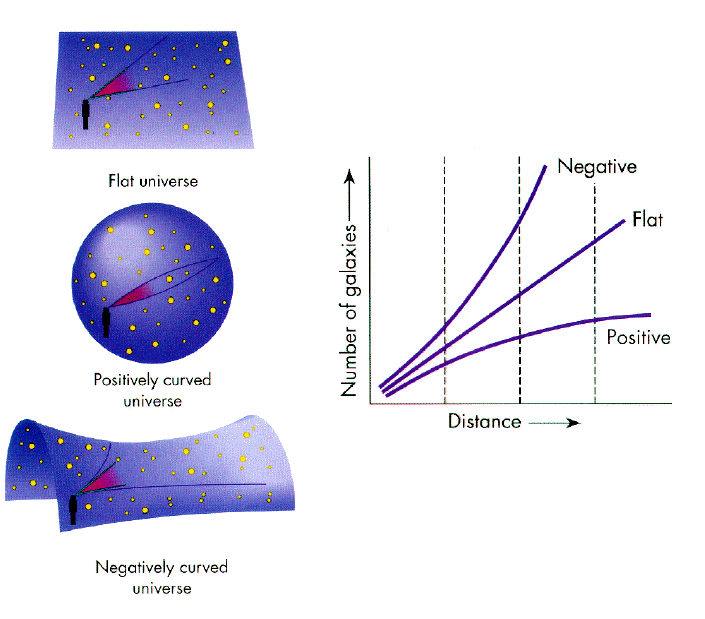
And just like how we can study how energy and matter are shaped or configured in our external reality (since this allows us to explain how things like light or heat travels or propagates), so too can we study how internal information, thoughts, values, rewards, beliefs, and maybe even Self-Awareness itself are arranged and shaped inside our Minds.

So what’s special about Hyperbolic geometry? Remember how I said that lines begin to radiate outward to form semi-circles in the upper half plane model like the wall in the background? In the upper half plane model (or projection), the geodesics can either form a single straight line going up from the middle (depending upon where we place our point-source of light), or meet once at the boundary (from which it then radiates outward and forms a semi-circle), or meet 0 times.
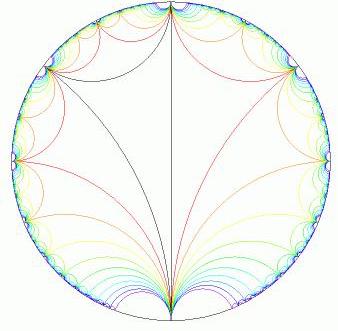
It turns out that in Hyperbolic geometry, as we go outward we have the property that we encounter exponentially more infinite space, making the Hyperbolic plane much much larger than the Euclidean plane, as well as tremendously easy to get lost in (eg - in order to walk from the center of a unit disc to the perimeter, it is an infinite distance away).

Because there are many more degrees of freedom, you allow patterns and structures with incredibly high degrees of branching. In physical models, this would take the form of exponentially more area in the surrounding edges, turning a normally flat disc into one where the edges are highly buckled and “frilly”, with lots of saddle points (think like a pringles potato chip or piece of lettuce for each saddle point), basically granting you increasingly more surface area (and evolution knows well the benefits of increasing surface area when it comes to resource exchange, metabolic waste, and heat dissipation).
Thinking about the structure of the brain now, could perhaps the physiological increase of surface area from which our cortical homunculus is mapped to, then potentially have downstream effects into one’s psychological inner mental space that they navigate through?
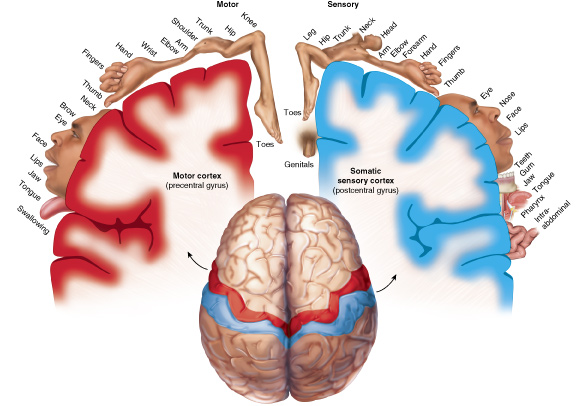
We know from differential geometry that “locally” (ie - “zoomed in”) we perceive a hyperbolic surface as Euclidean or flat, but globally it is not (similar to how we locally perceive the earth as flat, when globally it is not).
Could this be why we think that we think in Euclidean terms, due to computational time constraints of perceiving and acting on information in real life, whereas perceiving and acting on information in dream states are quite different experiences? (or similarly under the influence of certain drugs or neuropsychological conditions like when one experiences Alice-in-Wonderland Syndrome and one’s perception of sizes are greatly enlarged or made smaller).

Could this also be investigated empirically? We can maybe come up with interesting potential perceptual experiments by first coming up with thought experiments of what it would be like from the perspective of an observer living inside a Poincare disc (a unit disc composed of a hyperbolic plane), versus the perspective of an observer from an external outside Euclidean view.

Because we know that the distances inside the disc appear equal to an outside Euclidean observer whereas within the Hyperbolic plane they get infinitely longer the closer you are to the edge of the disc, then if we were a person living within the hyperbolic plane moving from the left to the perimeter, from the perspective inside the disc we’d be moving at a constant speed and never approach the edge, where from an outside Euclidean observer it would look like we are actually slowing down the more we travel to the edge. From the outside we see boundaries and time slowing down, whereas from the inside we see infinite space and time staying constant. Perhaps we can design experiments that can differentiate between these perceptual differences in time, speed, and limits?
Here are some interesting references which discuss more about Hyperbolic Geometry…
Playing sports in hyperbolic space by Numberphile
Exploring Hyperbolic Space w/ VR + Crochet *This one is really fun and good for building visual + physical intuition! (And if you are like me, you might become topologically ill, haha)
The Hyperbolic Geometry of DMT Experiences
A world that is shaped as a hyperboloid in the sci-fi book Dichronauts by Greg Egan
Excellent writeup on life on a Poincaré Disk
Documentary on famous geometer, Donald Coxeter, featuring his collaboration with famous artist M.C. Escher on the Poincaré disk model and Escher’s circle limit pieces. Also features many of my favorite mathematicians like John Conway, Benoit Mandelbrot, and Jeffrey Weeks (the latter who wrote an excellent book called The Shape of Space: How to Visualize Surfaces and Three-dimensional Manifolds that I review here)
And for those following my previous posts, particularly that of living systems and toroidal geometries, here’s a connection between hyperbolic geometry and the double (or generally 1+n holed) torus
And special thanks to mathematician Henry Segerman for his beautiful geometric shadow art and wonderfully intuitive explanations of geometry & topology using 3D printed models and light projections


